Skip to main content

Harmonics

sweet spot but no magic

I saw this diagram around 1961 (so obviously in a book) that demonstrates why certain pairs of notes harmonise harmoniously. The idea is that it is a representation of a continuous note played (the blue line in the diagram at right) while a second note starts at the same pitch and gradually increases up to the octave above (the red line).
So at any point the two notes and their octave harmonics add and subtract from each other to produce a jumble of pitches shown in the diagram below. I don't know what the book was. I must have borrowed it at the library. I've searched for the diagram but can't find it so made this one using the Numbers spreadsheet on a Mac.

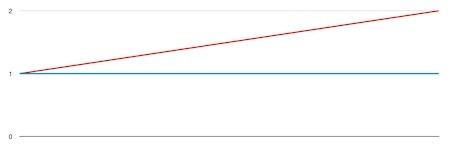
The two notes that combine to produce all the harmonics shown in the diagram below. The x axis is time and while a C sounds the whole time, another note is played starting at the same C and rising with time to the C one octave above.

Harmonic diagram showing natural harmonies as a constant C note is played along with a note that rises one octave starting and ending on C

At most frequency combinations there's a cacophony of sounds, but at some frequencies of the gliding "red" note there is a more pleasant combination. These frequencies can be seen on the second diagram as lighter paths "through the noise". Obviously you wouldn't be hearing most of the higher frequency combinations as they'd be faint and beyond the range of pitches we can hear but I plotted them so it's easier to see the "paths through the noise".

I plotted + tick marks at the bottom to show the frequencies of the consecutive notes of the western even ratio scale (the 12 tone equal temperament scale) and I've labelled some of them with note names assuming that the "drone" note (the blue one) is "C". You can see that F and G coincide closely with the natural harmonics. E and A coincide less closely.

All very mathematical and no magic involved. Obviously the natural F has 4 cycles to every 3 cycles of C (the compromised logarithmic scale approximates this at 1.3348) while the natural G has 3 cycles to every 2 cycles of C (approximated by 1.4983). Not quite a coincidence as the number of steps (12) had to be chosen but it's a happy coincidence that it worked out without having to go beyond 12. Happy but not magical.